Need to be fixed, rewrite when learning VAE
Refer to
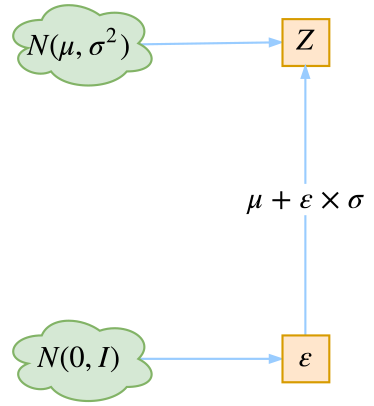Figure 1: Reparameterization Trick illustration
Simple Example
Assume we define
\[\begin{aligned} x \sim f_X(x)\\ y = h(x); \\ x = g(y) = h^{-1}(y) \\ \end{aligned}\]where h is a strictly increasing continuously differentiable function
Then we can have the desensity function \(f_Y(y)\) as by change of variable
\[\begin{aligned} f_Y(y) = f_X(x)|\frac{dx}{dy}| =f_X(g(y))g'(y) \end{aligned}\]Now we use normal distribution (as nice propety applied) and define
\[\begin{aligned} x \sim \boldsymbol{N}(\mu, \sigma^2)\\ y = h(x) = \frac{x-\mu}{\sigma}\\ x = g(y) =\sigma y+\mu \end{aligned}\]Therefore, we can have \(g'(y) = \sigma\) and apply the gaussian density function \(\boldsymbol{N}(g(y)|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2\sigma^2}(g(y)-\mu)^2)\)
s.t.
\[\begin{aligned} f_Y(y) &= f_X(g(y))g'(y) \\ &= \frac{1 \sigma}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2\sigma^2}(g(y)-\mu)^2) \\ &= \frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2\sigma^2}(g(y)-\mu)^2) \\ &= \boldsymbol{N}(0,1) \end{aligned}\]Therefore, we can map \(\boldsymbol{N}(\mu,\sigma^2) \rArr \boldsymbol{N}(0,1)\) with \(x = \sigma y + \mu\)
Reparameterization trick
Therefore, we can apply reparameterization trick in VAE and diffusion.
We want to minimize the loss by computing:
\[\nabla_\theta\mathbb{E}_{x\sim p_\theta (x)}[f(x)]\]Sometime the function above is not differentiable. We introduce a new variable & map through a determinstic function by substitution:
\[\begin{aligned} \epsilon &\sim p(\epsilon) \\ x &= g_\theta(\epsilon) \\ \therefore \nabla_\theta\mathbb{E}_{x\sim p_\theta (x)}[f(x)] &= \nabla_\theta\mathbb{E}_\epsilon[f(g_\theta(\epsilon))] \\ &= \mathbb{E}_\epsilon\nabla_\theta[f(g_\theta(\epsilon))] \end{aligned}\]By this method, we can now compute the gradient.
Remark
Andy said an non differentiable function cannot be differentiable by change of variable due to regularity.
In paper VAE (Kingma et. al, 2013) said reparameterization trick is used to generate a Monte Carlo estimater to estimate the gradient, which is no way to differentiate (although you know it is differentiable).
However, in deep learning we use back-propagation instead of taking sampling. The sampling steps for Monte Carlo estimator will not happen. So what is the real trick in VAE?
